研究网衣流场特性通常可以采用模型试验和数值模拟两种方法。虽然模型试验可以进行养殖网箱网衣流场的分析,但成本高,且受试验场地的限制。随着计算流体力学(Computational fluid dynamics, CFD)的不断发展,CFD技术已能较为准确地分析一些流体力学问题,不仅能得到养殖网箱整体受力情况,还可以捕捉养殖网箱内外流场的细节。桂福坤[5]对深水重力式网箱的水动力特性开展了模型试验,给出了重力式、碟形及拟碟形网箱的受力及运动特性;Patursson O等[6-7]对平面网衣的流场进行了模型试验和数值模拟,测量了网衣的阻力系数及升力系数,模拟了网衣后面的流场速度分布;赵云鹏等[8-9]借助商业软件FLUENT对单片网衣周围的流场特性进行了二维数值模拟,结果表明:FLUENT中的多孔介质模型可以用于网衣周围流场的数值模拟;刘兴[10]采用多孔介质模型,分别对平面网衣的流场进行了二维和三维数值模拟,结果表明:三维数值模拟的误差更小;刘春宏等[11]对网衣和鱼类共同作用下的网箱周围流场进行了数值模拟,发现需同时考虑鱼类和网衣才能准确地模拟养殖网箱周围的流场。
为研究及分析养殖网衣周围的流场特性,本文基于CFD理论,采用多孔介质模型对单片网衣的流场进行数值模拟,首先进行不确定度分析,再对网衣在不同流速下的流场进行数值计算,并与试验结果进行了比较,最后对网衣在不同攻角下的流场进行数值计算,分析了网衣的流场特性,给出网衣对流场内速度影响的量化区域及范围,旨在能够较好地为实际养殖生产活动提供参考依据。
1 理论模型
1.1 控制方程
流体力学问题要遵守质量守恒、动量守恒和能量守恒定律,对于不可压缩流体,其连续性方程和动量守恒方程分别如下[12]:
式(1)~(2)中:ui和uj为速度;xi和xj为坐标分量;t为时间;p为流体的压力;ρ为流体的密度;μ为流体的黏性系数。
控制方程不封闭,因而需引入湍流模型,使方程能够求解。本文计算采用标准k-ε湍流模型[12],该模型具有较髙的稳定性、经济性和计算精度,应用广泛,其表达形式如下:
式(3)~(4)中:k和ε分别为湍动能和耗散率;μt为湍流黏性系数;Gk和Gb分别为平均速度梯度和浮力引起的湍动能产生项;σk和σε分别为k和ε的普朗特数。常数σk=1.0、σε=1.3、
1.2 多孔介质模型
将养殖网衣视为多孔透水板,采用多孔介质模型进行数值模拟。在数值模拟中,以动量方程的右边增加源项来模拟多孔介质,动量方程[13]变为:
式(5)中:Si为源项,其表达式为:
式(6)中:Pν和Pi分别为多孔介质黏性力系数矩阵和惯性力系数矩阵。
水流作用在多孔介质区域的合力(F)[13]为:
式(7)中:t为多孔介质的厚度;A为多孔介质的面积。
式(8)~(9)中:
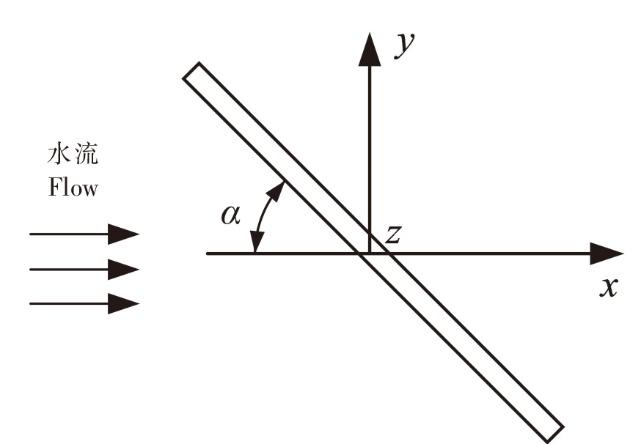
图1
网衣密实度(S)的表达式[13]为:
式(10)中:d为网线直径;λ为网目长度。
网衣密实度与多孔介质孔隙率的关系为:
式(11)中:χ为多孔介质的孔隙率。
2 数值计算方法
2.1 计算模型
表1 网衣的尺寸
Tab.1
| 名称Name | 参数Parameter |
|---|---|
| 网衣长度/m Net panel length | 1.0 |
| 网衣宽度/m Net panel width | 1.0 |
| 网线直径/mm Net line diameter | 2.8 |
| 网目长度/mm Net mesh length | 29.0 |
| 网衣密实度Net panel compactness | 0.198 |
| 网衣材质Net panel material | 尼龙 |
| 网衣类型Net panel type | 无节网 |
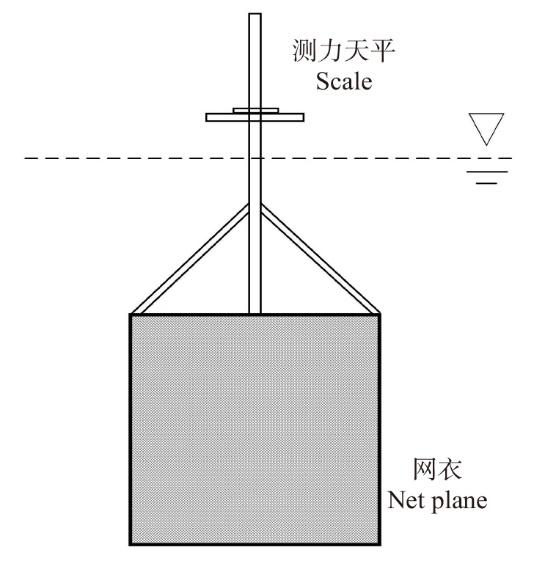
图2
2.2 网格生成
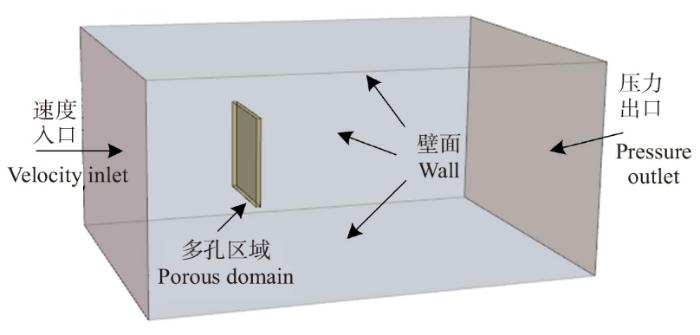
数值计算的计算域和边界条件如图3所示。计算域的长度为5 m,宽度和高度与试验水槽相同,多孔介质模型距离进流面入口1.5 m,多孔区域厚度为0.05 m。计算域的边界条件设置如下:进流面设置为速度入口条件;出流面为压力出口条件;水槽四周为无滑移壁面条件;水槽与多孔区域的交界面为内部界面条件。
图3
数值计算采用的网格类型为非结构切割体网格。在网衣周围区域和网衣后侧区域进行了网格细化,用于捕捉网衣后侧的流场。计算域的总网格数为31×104,其中加密区域1和加密区域2的网格为18×104和8×104。整体计算域网格和中间水平截面网格如图4所示。
图4
2.3 计算方法
在数值计算中,求解器采用基于分离流的黏性求解器,压力速度耦合算法为SIMPLE法,对流项采用二阶离散格式。湍流模型采用标准k-ε湍流模型,壁面函数采用高y+壁面处理。采用三维定常计算,最大迭代步数为1 000步。
对网衣试验结果进行拟合,多孔介质的法向惯性系数和切向惯性系数分别为2 492.5、830.0kg/m4,法向黏性系数和切向黏性系数分别为75.08、38.31kg/(m3·s)[9],多孔介质的孔隙率为0.802。
3 数值计算结果
3.1 不确定度分析
网衣阻力系数和升力系数的定义[13]为:
式(12)~(13)中:Cd为网衣阻力系数;D为网衣所受的阻力;Cl为网衣升力系数;L为网衣所受的升力。
表2 网格的计算结果
Tab.2
| 名称 Name | 网格尺寸/m Mesh size | 网格数量/×104 Mesh number |
|---|---|---|
| 网格1 Mesh 1 | 0.100 | 31.7 |
| 网格2 Mesh 2 | 0.142 | 12.2 |
| 网格3 Mesh 3 | 0.200 | 4.4 |
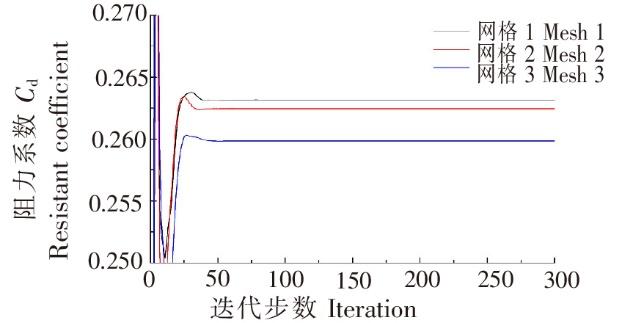
图5
图5
不同网格尺寸下的网衣阻力收敛曲线
Fig.5
Convergence curves of the net panel resistance at different mesh sizes
可以看出,3套网格在数值迭代计算75步后,网衣阻力都已经完全收敛,将数值模拟的总迭代步数设置为75~100,可节省计算工作量。1号网格、2号网格和3号网格的网衣阻力系数分别为0.263、0.262和0.260。采用国际拖曳水池(ITTC)的不确定计算方法对网衣阻力进行不确定度分析,不确定度分析分为验证与确认两个过程[14]。
1)验证
数值不确定度由迭代不确定度(UI)、网格不确定度(UG)以及其他因素的不确定度(UP)组成。本文数值模拟采用定常计算,网衣阻力曲线几乎无波动,迭代误差可以忽略不计,验证过程主要为计算数值模拟中的网格不确定度UG。
网格的收敛半径RG为:
式(14)中:ε21为细网格与中网格的差值;ε32为中网格与粗网格的差值。
网格收敛半径为0.281,0<RG<1,网格收敛条件为单调收敛,可使用Richardson 外插法分析其不确定度:
式(15)~(18)中:PG为准确度量阶;
网衣流场数值模拟的不确定度分析结果为:准确度量阶PG=3.661;误差的单项估计值
2)确认
确认是利用试验数据来评估数值模型不确定度USN的过程,将数值模拟值(S)与试验值(D)进行比较。
式(19)~(20)中:E为比较误差;UV为数值结果确认过程的不确定度;UD为试验结果的不确定度。
当
网衣阻力系数的试验值D=0.257,数值模拟与试验值的对比误差E=2.32%,通常假设试验误差UD=5%,确认不确定度UV=
3.2 不同流速下的计算结果
在来流为0.125、0.250、0.500和0.750 m/s等4个速度下,对攻角为90°的网衣流场进行数值模拟,并与Patursson O的网衣阻力试验结果[6]进行比较,以验证数值模拟方法的准确性及有效性。
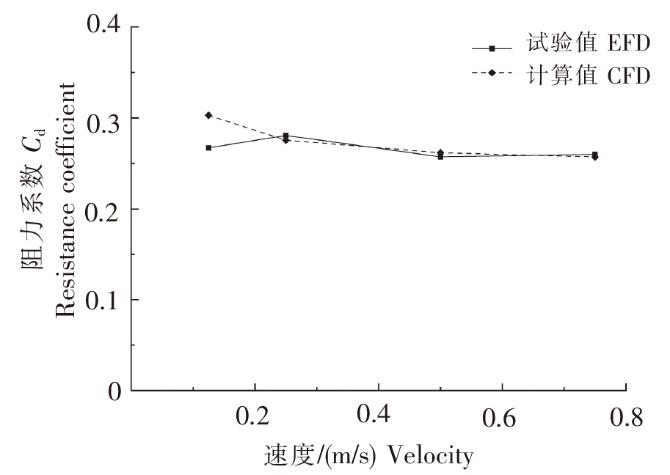
网衣阻力系数计算结果和试验结果对比如图6所示。由图可见,当来流为0.125 m/s时,网衣阻力的数值模拟结果偏大,误差为13.4%,主要原因为低速时网衣阻力的数值较小,相对误差较大;当来流分别为0.250、0.500和0.750 m/s时,网衣阻力的误差分别为-1.85%、1.75%和-1.11%。整体上,网衣阻力的数值模拟结果与试验结果吻合良好,说明本文数值模拟方法有效,可用于养殖网箱流场的数值预报。
图6
图6
不同速度下的网衣阻力计算值与试验值对比
Fig.6
Comparison of the calculated and experimental resistance values at different velocities
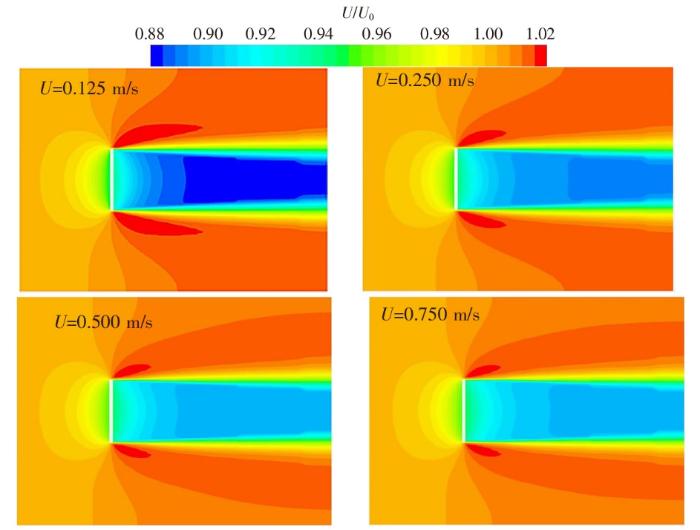
图7
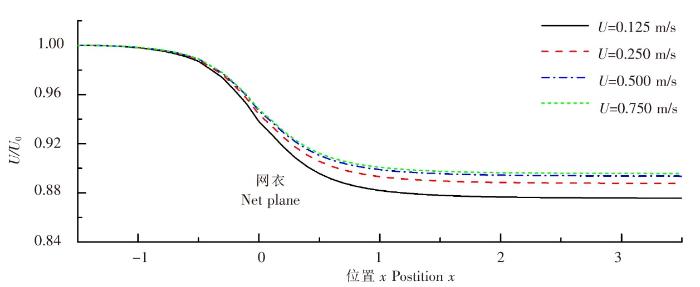
图8
图8
不同流速下网衣中心前后的速度分布
Fig.8
Velocity distribution before and after the center of the net at different flow velocities
3.3 不同攻角下的计算结果
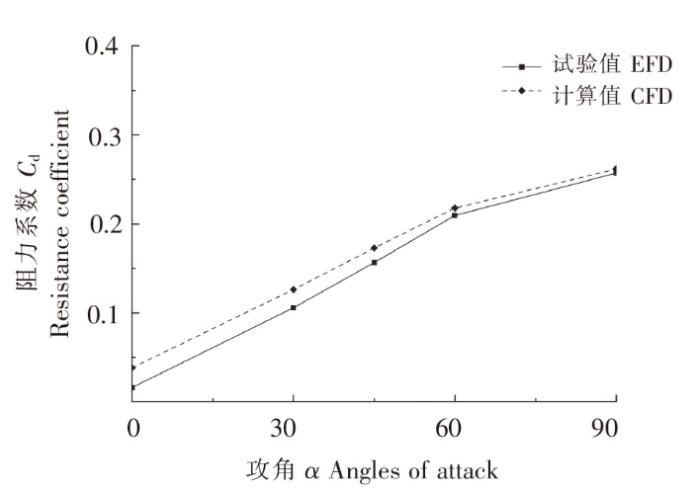
图9
图9
不同攻角下的网衣阻力计算值与试验值对比
Fig.9
Comparison of the calculated and experimental resistance values at different angles of attack
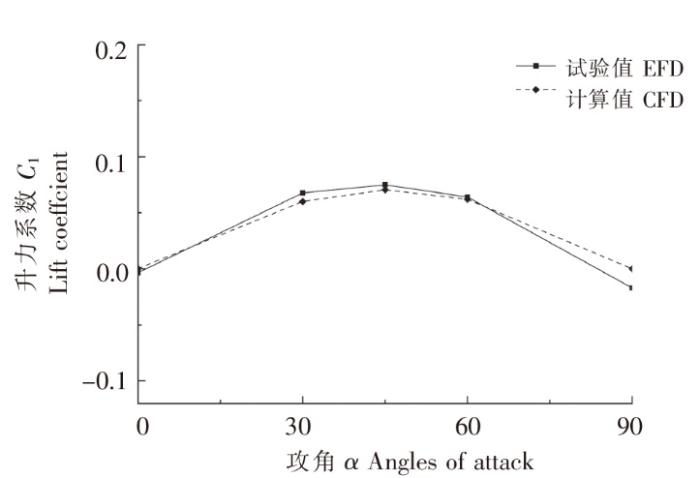
图10
图10
不同攻角下的网衣升力计算值与试验值对比
Fig.10
Comparison of the calculated andexperimental lift values at different angles of attack
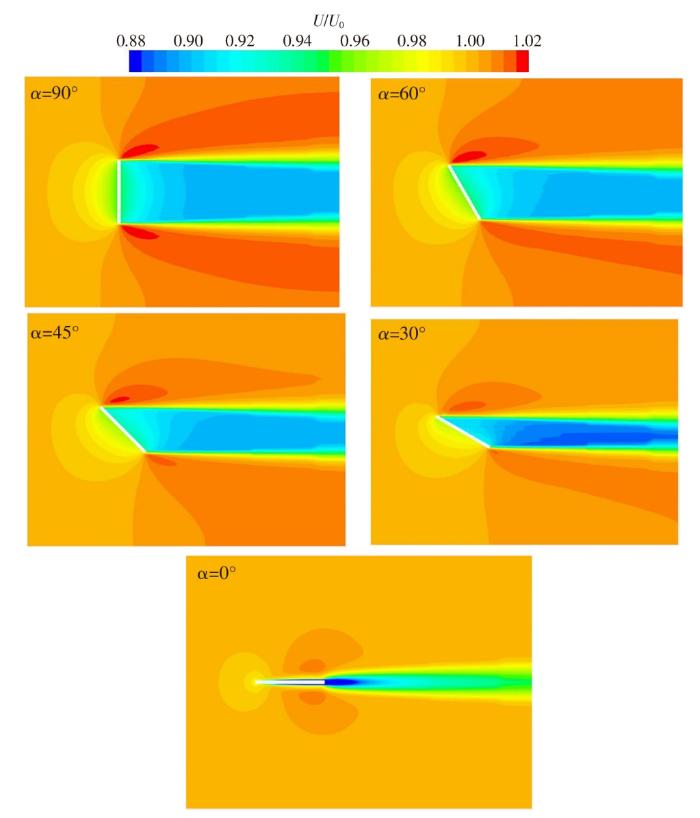
图11
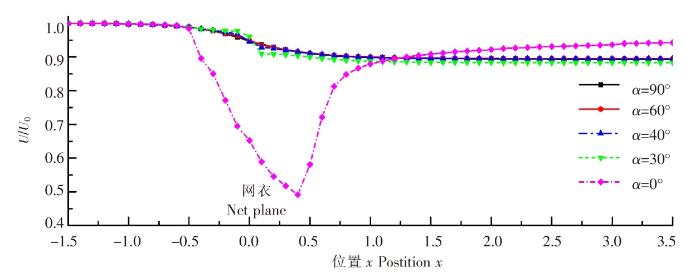
图12
图12
不同攻角下网衣中心前后的速度分布
Fig.12
Velocity distribution before and after the center of the net at different angles of attack
4 结论
本文基于CFD理论,采用多孔介质模型对单片网衣的流场进行了数值模拟,首先进行了不确定度分析,然后对网衣在不同流速和不同攻角下的流场进行了数值计算,再将数值计算结果与试验结果进行了对比,并对网衣流场特性进行了分析。结果如下:
1)网衣阻力和升力的数值模拟结果与试验结果吻合良好,说明本文数值模拟方法有效,可用于养殖网箱流场的数值预报。
2)在网前0.5倍网衣长度到网后1.0倍网衣长度的范围内,流体速度下降较快,网衣对流体有明显的阻挡作用;当超过1.0倍网衣长度时,流体速度基本不再变化。
3)随着来流速度的增加,网衣后方对来流速度的阻挡作用逐渐减弱。
采用本文数值模拟方法可以准确获取网衣周围的流场数据,在后续工作中,将进行本文数值模拟方法与网衣变形程序之间相互耦合的研究,从而可对具有百万级网目的柔性网衣进行求解。
参考文献
港湾海域新型网箱养鲍新技术探讨
[J].根据鲍的生活习性,总结国内外养鲍设施特点,自行研发新型竖排式网箱。通过在港湾海域进行新型竖排式网箱的养鲍试验,对养鲍过程中网箱内饵料分布、附着生物情况进行研究,并与传统挂笼养殖模式对比分析。結果表明:新型网箱养殖过程中采用平潮点倾倒法投喂龙须菜或海带,鲍匍匐基内的饵料占比分别为:龙须菜约30.4% ,海带约36.7% ,均高于其它投喂方式。经过9个月的养殖,网目为1 cm的竖排网箱中的鲍最终体重为(29.1±6.17)g,存活率为60.5%,传统挂笼中鲍体重为(22.8 ±7.93)g,存活率为33.5%,新型网箱养殖效果显著优于传统挂笼(P0.05),但均显著大于传统挂笼组(P<0.05),进入夏季后,网箱中附着生物的生物量和丰富度都有显著增加。与传统挂笼相比,新型竖排式网箱具有水体交换好、操作简单、节省劳力、存活率高等优点。
浅论我国大黄鱼产业转型升级之对策
[J].经过30多年的研究与发展,我国大黄鱼产业已进入转型升级阶段。本文就加快大黄鱼原良种体系建设、规范养殖网箱布局和优化网箱结构、提高养殖经济效益与产品质量、加快全价人工配合饲料研发与推广应用、实施鱼病综合防控技术、提高产品加工率、实施品牌战略、进一步发挥行业协会作用、发掘大黄鱼文化等方面,论述了我国大黄鱼产业转型升级的对策。
“云龙石斑鱼”深海网箱养殖试验
[J].放养平均全长(29.95±2.51)cm、平均体重(357.00±8.31)g和平均全长(11.63±1.13)cm、平均体重(19.85±1.23)g两种规格的云龙石斑鱼(云纹石斑鱼♀× 鞍带石斑鱼♂)鱼种进行深海网箱养殖试验。试验期水温为14.2~29.2℃,投喂含46%~48%粗蛋白的石斑鱼配合饲料,经12个月饲养,大规格云龙石斑鱼平均体重达(1 650.22±20.23)g、平均全长达(44.72±3.73)cm,小规格云龙石斑鱼平均体重达(480.20±22.32)g、平均全长达(32.41±3.53)cm,饲料系数为1.22。大规格云龙石斑鱼体重和全长的最优回归方程为幂函数方程W=0.001L3.667,小规格云龙石斑鱼体重和全长的最优回归方程为幂函数方程W=0.011L3.142。云龙石斑鱼深海网箱养殖最适水温为21.2~28.7℃。试验结果表明云龙石斑鱼适合福州深海网箱养殖。
Development of a porous media model with application to flow through and around a net panel
[J].
Numerical simulation of the flow around fishing panel nets using the porous media model
[J].
Numerical simulation of the interaction between flow and flexible nets
[J].